熵
熵是衡量某个体系中事物混乱程度的一个指标,是从热力学第二定律借鉴过来的。
熵增原理
孤立系统的熵永不自动减少,熵在可逆过程中不变,在不可逆过程中增加。
[来自百度百科]
熵增加原理是热力学第二定律的又一种表述,它更为概括地指出了不可逆过程的进行方向;同时,更深刻地指出了热力学第二定律是大量分子无规则运动所具有的统计规律,因此只适用于大量分子构成的系统,不适用于单个分子或少量分子构成的系统。
Consul为什么要反熵
举个现实社会的例子,国家是由一个个的人组成的,小国家几万人口,大国家几亿人口,每个人都有自己的想法,不可能这些人没有组织就能维持这个国家的运转。我国有省市县乡四级行政区划,乡管理几十个村,县管理十几个乡,市管理十几个县,省管理十几个市。如果让省直接去管理以万为单位的村,李村的村长贪污了补贴款,张村的马路被压坏了,隔壁王村放开二胎后还是没人生孩子…,肯定是管不过来的。通过这种层级的行政划分,国家得到了有序的治理,而不是乱哄哄一片。
Consul面对的问题也是类似的,它是一个分布式的服务发现系统,需要做服务注册、健康检查、服务发现,以及在成员之间共享这些服务信息。大点的系统可能有成千上万的服务,分布在成百上千的节点,服务应该注册在哪些节点,数据在节点之间怎么同步,节点失败了怎么办,怎样保证增加节点数量不会导致性能明显下降…如果不解决好这些问题,整个系统可能就会变得混乱,走向失控和崩溃。
理解两个组件
这里首先介绍跟服务和健康检查紧密相关的两个部件:Agent和Catalog,可以让大家更容易理解Consul的反熵。
Agent
Agent存在于Consul的每一个节点中,负责维护注册到其上的服务和健康检查,以及执行这些健康检查,更新本地服务的健康信息。
Catalog
Catalog存在于Server 节点,聚合了各个Agent采集的信息,包括服务、健康检查、相关的节点,以及它们对应的状态,服务发现就是基于Catalog来做的。
然而Catalog中这些信息的字段要比Agent维护的少很多,因为Catelog只是一个视图,它没有关于服务、健康检查和节点的设置项信息。
反熵机制
根据前边对熵的说明,Consul 的反熵就是让Consul集群更有序,而其反熵机制就和上边提到的两个部件紧密相关。
当服务或健康检查在Agent注册后,信息就会通知到Catalog中;当Agent中根据健康检查的服务状态发生变化时,状态也会通知到Catalog中;当服务或健康检查从Agent中消失后,Catalog中也会移除相对应的信息。
Agent负责注册到其上的服务及健康检查,Catalog负责聚合集群各个Agent的数据用于服务发现,Agent同步最新数据到Catalog,各个Agent的数据不断收敛到Catalog,从而实现集群的有序运作。波斯码建议大家通过调用Consul API中的Agent和Catalog接口来验证这个机制。
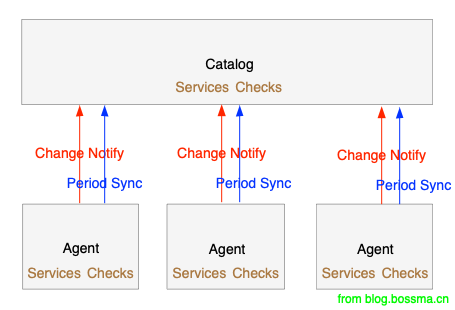
周期同步
除了当变化发生时Agent主动通知外,Agent还有一个定时器执行到Catalog的完整同步操作。极端情况下,如果在Catalog中移除了某个Agent的所有信息,过一会这些信息也会重新同步到Catalog中。为了降低同步可能导致的并发影响,针对不同的集群规模默认了不同的同步周期:
| 集群规模 | 同步周期 |
|---|---|
| 1 – 128 | 1 minute |
| 129 – 256 | 2 minutes |
| 257 – 512 | 3 minutes |
| 513 – 1024 | 4 minutes |
| … | … |
这个同步间隔只是一个近似值,为了防止大量节点同时同步导致惊群效应,实际程序中会在同步周期内引入一个随机值来错开同时请求。
同步的异常处理
同步的时候可能会出现各种问题,比如Agent配置错误、磁盘满了、没有写入权限、网络不通等等,出现这些问题时,Agent会记录日志后继续运行,然后等待下一次周期同步尝试。
启用Tag Override
如果开启这个选项,则Agent同步数据到Catalog时,将不会同步服务的tag数据。举个实际的例子:主从部署的redis,使用sentinel监控实例的状态,如果主redis下线,则某个从redis升级为可写的主实例。假设使用服务的tag作为主从的标识,这里就不能使用服务注册时的tag,而应该通过sentinel获取redis实例的主从状态,然后设置到Catalog中,服务发现才能获取到当前实际的redis主实例。
这篇文章由Consul官方文档整理而来,加入了波斯码个人的一些理解。点此查看原文。
发表评论
相关文章
国内AI资源汇总,AI聊天、AI绘画、AI写作、AI视频、AI设计、AI编程、AI音乐等,国内顺畅访问,无需科学上网。
扫码或点击进入:萤火AI大全
文章分类
最新评论